
Sine Movement
Calculation of hydraulic cylinders, oscillation cylinders
The simplest harmonic sine movement of a controlled cylinder axis is a cyclical extension and retraction of the piston rod. However, completely irregular travel profiles can also be mathematically described by basing a sine movement on each point.
The simplified calculation integrated in the HäKo product configurator (test actuator >> hydraulic calculation) is used to design a dynamic movement in sine operation. Above all, cylinder data is taken into account, but other system-relevant parts such as hoses or valves and their leakages are not included.
The sine movement is defined by entering the amplitude and frequency. The calculation then determines the respective maximum values of the movement, which, however, do not occur simultaneously in a sinusoidal oscillation. For example, the speed has its maximum value at the moment when the acceleration value is zero.
This is sufficient for a typical design to determine the cylinder size.
This calculation does not replace the simulation of the complete hydraulic system, which is necessary in special cases, for example, when the system reaches its design limits.
The calculation is used to design a movement in sine wave operation. It does not include the behaviour when the hydraulic plant is switched on or off.
Force calculation
The cylinder force Fb at working pressure is the force that is achieved in dynamic operation. Working pressure refers to the actual pressure pb prevailing in the cylinder chamber, which is set behind the control valve.
Fb = pb • A
with the effective piston area from bore D2K and piston rod diameter d2s
A = π / 4 • (D2K - d2s)
The cylinder force Fs at system pressure is the force that is achieved in static operation. System pressure refers to the pressure ps prevailing in front of the control valve, which is provided by the power unit.
Fs = ps • A
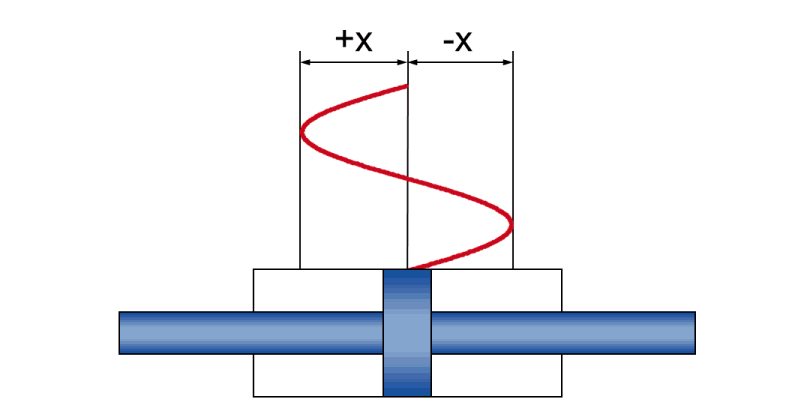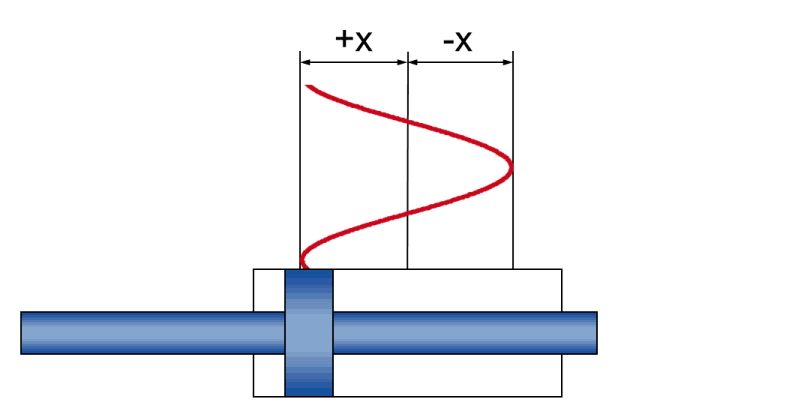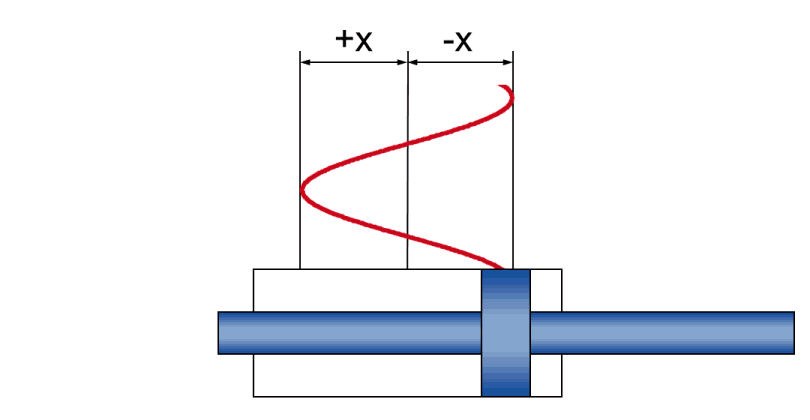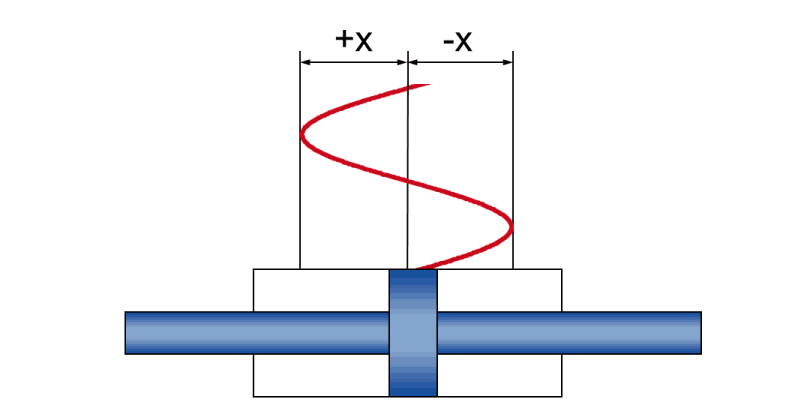
Dynamic Sine Movement
In dynamic operation, physical relationships result from a sine movement between
- Amplitude +/- x - the actual stroke movement during the oscillation
- speed v - the instantaneous (and constantly changing during the oscillation) piston speed
- acceleration a - the instantaneous (and constantly changing during the oscillation) piston acceleration
- frequency f - the time sequence of the stroke movement, specified as the number of oscillations per unit of time
| Maximum values |
| v = 2 π f x |
| a = 4 π2 f2 x |
This results in the max. flow rate Q required for the movement
Q = v • A
with the effective piston area A
A = π / 4 • (D2Piston - d2Rod)
and the accelerating force Fa to be provided by the cylinder
Fa = m • a
From the maximum acceleration calculated here and the moved mass, an accelerating force results, which the cylinder must apply. The dead weight of the piston rod is taken into account in the calculation program; additional moved masses must be specified in the corresponding field.
Servo valve recommendation
The system pressure ps is calculated taking into account the pressure drop Δp in the control valve as follows:
pb = ps - Δp
The pressure drop of the control valve is usually specified as 70 bar for servo valves or 10 bar at nominal flow rate. In operation, however, this depends on the actual flow rate.
According to the required flow rate, the program suggests a nominal flow rate for a possible control valve. The pressure drop is then also calculated for this. This is intended to quickly provide an overview of which size class of valve would be required.
The leak oil flow of the sealing system and the servo valve must be added to the calculated flow rate value.
A precise valve determination and design remains unaffected by this design.
Further calculation formulas for the design of hydraulic cylinders:
Calculation formulas for the design of hydraulic cylinders
Calculation of permissible oil speeds
Calculation of the buckling resistance of hydraulic cylinders
Buckling cases calculation - Mountings of piston rod and cylinder